Exponential Growth And Decay Modeling Data

Exponential Growth And Decay Modeling Data. In this section, we will study some of the applications of exponential and logarithmic functions. Exponential decay modeling with mathematics to be profi cient in math, you need to apply the mathematics you know to solve problems arising in everyday life.

PPT Exponential Growth & Decay Modeling Data PowerPoint from www.slideserve.com

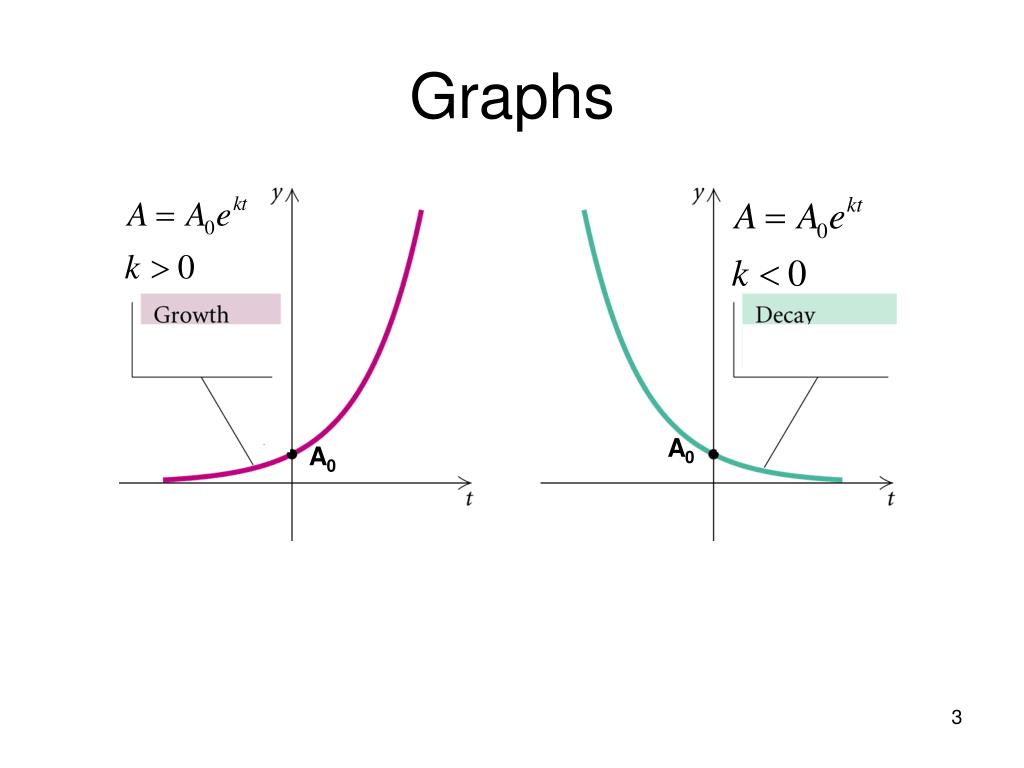
But sometimes things can grow (or the opposite: This can be done with exponential growthand decay models.with exponential growth or decay, quantities grow or decay at a rate directly proportional to their size. Atmospheric pressure of air at a certain height;

Source: aire-nc.org

For example, if a bacteria population starts with 2 in the first month, then with 4 in the second month, 16 in the third month, 256 in the fourth month, and so on, it means that the population grows exponentially with a power of 2 every month. This can be done with exponential growthand decay models.with exponential growth or decay, quantities grow or decay at a rate directly proportional to their size.

Source: www.differencebetween.net

If 0 < b < 1, 0 < b < 1, the function models exponential decay. Exponential growth and decay hhsnb_alg1_pe_0604.indd 313snb_alg1_pe_0604.indd 313 22/5/15 7:50 am/5/15 7:50 am

Source: www.youtube.com

But sometimes things can grow (or the opposite: Modeling data about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new.

Source: www.youtube.com

Population growth of bacteria, viruses, plants, animals and people; Such models are based upon empirical data.

Source: studylib.net

Graphing experimental data might reveal exponential growth or decay. This can be done with exponential growthand decay models.with exponential growth or decay, quantities grow or decay at a rate directly proportional to their size.

Source: serc.carleton.edu

Model exponential growth and decay. Populations that are growing exponentially grow extremely rapidly as they

Source: www.slideserve.com

K = rate of growth (when >0) or decay (when <0) t = time. In fact, by looking at data complied by the national.

Source: mungfali.com

A 0 is the original amount, or size, of the growing entity at time t=0, a is the amount at time t and k is a constant representing the. The model is nearly the same, except there is a negative sign in the exponent.

Examples Of Data That Fit Exponential Decay Are:

12.5 exponential growth and decay; Graphing experimental data might reveal exponential growth or decay. Such models are based upon empirical data.

If B > 1, B > 1, The Function Models Exponential Growth.

Today i’m sharing a creative way to use candy (in this case skittles) for a modeling exponential growth and decay activity in algebra. This can be done with exponential growth and decay models. In fact, by looking at data complied by the national.

This Can Be Done With Exponential Growthand Decay Models.with Exponential Growth Or Decay, Quantities Grow Or Decay At A Rate Directly Proportional To Their Size.

$ a_{0}$ is the original amount, or size, of the growing entity at time t = 0, $ a $ is the amount at time $ t $, and $ k $ is a constant representing the growth rate. Exponential functions can also be used to model populations that shrink (from disease, for example), or chemical compounds that break down over time. Students are using their knowledge of exponential growth and decay to research and model real population data.

Similarly, If The Growth Or Decay Factor Between Successive Points Is Not Constant, The Data Is Not Exponential.

In this section, we will study some of the applications of exponential and logarithmic functions. Modeling data about press copyright contact us creators advertise developers terms privacy policy & safety how youtube works test new. Atmospheric pressure of air at a certain height;

See Www.mathheals.com For More Videos

We say that such systems exhibit exponential decay, rather than exponential growth. Logarithms were invented by john napier. Model exponential growth and decay.